Jesteś rodzicem, jesteś nauczycielem -chcesz ochronić dziecko przed niepowodzeniem szkolnym przeczytaj ten artykuł.
Chcę pokazać jak kluczowe mogą okazać się zmiany sposobu nauczania w osiąganiu przez dzieci kompetencji w matematyce. Tym sposobem jest nauczanie przez doświadczenie. Prosty przykład.
Większość zaburzeń w uczeniu się matematyki jest konsekwencją zbyt szybkiego wymogu rozumowania operacyjnego bez odpowiedniego przygotowania dziecka oraz oderwania czynności matematycznych od życia codziennego i doświadczenia uczniów. Jeżeli twój uczeń/twoje dziecko nie jest gotowe stawić czoła problemom szkolnym to pod koniec tego artykułu dowiesz się jak mu pomóc.
To bardzo ważne! Gotowość szkolną można sprawdzić (na potrzeby artykułu) w jednym aspekcie operacyjnego rozumowania (fachowo się to nazywa-zakres ustalania stałości ilości nieciągłych)
Jedno zadanie z testu gotowości szkolnej

Jak to zrobić?
Przygotuj do tego klocki lego (5 dużych i 5 małych). Możesz klocki ustawić w taki sposób jak wykonano to na zdjęciu 1. Następnie poproś dziecko aby patrząc na te dwa zbiory określiło ile jest w nich klocków.

Zmień konfigurację tak jak na zdjęciu 2 i poproś o ponowne określenie liczebności zbioru.
Poziom gotowości szkolnej
1. Jeżeli twój uczeń/twoje dziecko znajduje się w grupie niskiego poziomu operacyjnego rozumowania, zachowa się następująco:
Po rozłożeniu klocków stara się je liczyć, a potem pada stwierdzenie: "tu jest więcej klocków", wskazuje na szereg klocków dużych.
Po zmianie układu klocków: "tu jest więcej" wskazuje obszar zajmowany przez klocki duże. Zapytane: "dlaczego tak uważasz?" Odpowiada najczęściej: "bo widać. Tutaj jest ich więcej. Tu pięć i tu pięć ale tu więcej".
Podstawą rozumowania jest zajmowana przestrzeń.
2. Jeżeli twój uczeń/twoje dziecko znajduje się w grupie średniego poziomu operacyjnego rozumowania, zachowa się następująco:Po rozłożeniu klocków, liczy po cichu, po każdej zmianie liczy ponownie a potem mówi: "jest tyle samo". Zapytane dlaczego?: "bo policzyłem, bo tak jest".
Dziecko nie potrafi jeszcze ujmować spostrzeganych zmian w układzie klocków jako odwracalnych. Dziecko jest zaniepokojone. Silna potrzeba liczenia krążków po każdej zmianie.
3. Jeżeli twój uczeń/twoje dziecko znajduje się w grupie wysokiego poziomu operacyjnego rozumowania, zachowa się
następująco:
Po rozłożeniu klocków liczy a później pewnie odpowiada: "musi być tyle samo, jest tyle samo". Kiedy nauczyciel/rodzic zapyta: "dlaczego tak uważasz", wyjaśni : "bo
jest tyle samo tylko je pani inaczej ułożyła".
Dziecko potrafi uznać obserwowalne zmiany w układzie i nie musi ich ciągle przeliczać. Cechę liczebności odrywa od wyglądu i przestrzeni zajmowanej przez
klocki.
Błędna lekcja

Może zdarzyć się tak, że twój uczeń/twoje dziecko nie osiągnęło należytych kompetencji intelektualnych do uczenia się matematyki. Nie jest to zmartwienie chyba, że...
Nauczanie rozpocznie się od sytuacji opisanej poniżej.
Nauczycielka przybliża uczniom liczbę 6. Zaczyna od ćwiczenia. Każde dziecko otrzymuje kartkę z rysunkami.
Nauczycielka: Pokażcie zbiory równoliczne. Pokażcie zbiory, w których jest tyle samo elementów.
Jak odpowie dziecko, które jest na niskim poziomie operacyjnego rozumowania?: "żyrafy są ogromne a motylki małe". Nie potrafi oderwać cech ilości od cech jakości. Ale to nie jedyny problem. Dziecko uważnie słucha i dopasowuje polecenie do swoich możliwości. Tak samo czynią to dorośli. Zawsze ważne są informacje i te najlepiej są kodowane, kiedy zbieżne są z naszymi doświadczeniami. Uczeń/dziecko podobnie widzi w zadaniu to, co jest zgodne z jego doświadczeniem i jego potrzebami.
Nauczycielka widząc, że duża część uczniów sobie nie radzi, proponuje takie rozwiązanie.
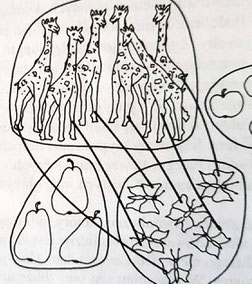
Nauczycielka widząc, że duża część uczniów sobie nie radzi, proponuje takie rozwiązanie. Przyjmuje taką strategię (fot. 4)
Narysowanie kresek niczego nie zmieni. "żyrafy są nadal duże a motylki małe i jeszcze są kreski, których jest jeszcze mniej". Ani żyrafa, ani motylki nie wychodzą poza swoje znaczenie. Nie są liczbami. Zresztą co ma żyrafa do motylków?
Wielu rodziców, nauczycieli nie przypuszcza nawet, że duża część dzieci interpretuje odmiennie treści zadań z uwagi na to, że funkcjonuje w innej konwencji logicznej. Najgorsze jest w tym to, że nie potrafi wyjaśnić swych wątpliwości, gdyż musiałaby to uczynić w kategoriach operacyjnych, a te są niedostępne.
Zanim dziecko zdoła oderwać czynności intelektualne od cech przedmiotów, musi doświadczać wielu sytuacji zbieżnych z możliwościami ich odbioru.
Bądź w miejscu, w którym są uczniowie
Bądźmy zatem „tam”, gdzie znajduje się nasze dziecko.
Jak wybudować doświadczenie?
Większość dzieci (doświadczenie musi być tak proste aby obejmowało jak największą grupę dzieci) wie jak zorganizować przyjęcie dla lalki, misia, zrobić napój w butelce, dżem. Zajęcia należy rozpocząć od czegoś tak banalnego, że niegodne jest uwagi (przykład) od przygotowania balu dla lalek. Ile potrzeba talerzyków, łyżeczek, kubków dla ustawionych lalek? Lalki duże, kubeczki małe a potrzeba ich tyle samo.
Można nawiązać do doświadczenia gotowania dżemów w słoikach. Jak przygotować dżem lub jak przygotować napoje na wycieczkę dla lalek, misiów?
Ile nakrętek potrzeba aby zakręcić dżem? Ile nakrętek potrzeba aby zakręcić butelki? Ważne aby dziecko "przygotowało dżem” i chciało przeliczyć ilość zakrętek, które będą potrzebne aby te dżemy zakręcić.
Ważne aby dziecko przygotowało butelki i zechciało przeliczyć ilość nakrętek?
Przykładów jest mnóstwo. Wszystko zależy od naszej fantazji.
Przykłady rysujemy na kartkach i rozdajemy dziecku. Prosimy o określenie ile jest lalek a ile talerzyków, czy wszystkim lalkom wystarczy talerzyków?
Proste prawda?

Write a comment